مسئله برج هانوی با پایتون

برج هانوی یک پازل ریاضی کلاسیک است که شامل جابجایی مجموعه ای از دیسک ها از یک میله به میله دیگر، با رعایت قوانین خاص است. در این برنامه پایتون، نحوه حل برج هانوی را با استفاده از بازگشت، یک تکنیک برنامه‌نویسی اساسی که به ما امکان می‌دهد این مشکل پیچیده را به زیرمسائل ساده‌تر و قابل مدیریت تقسیم کنیم، بررسی خواهیم کرد. این برنامه توالی حرکات مورد نیاز برای انتقال کارآمد دیسک ها بین میله ها را نشان می دهد و نمونه ای واضح از حل مشکل بازگشتی در عمل را ارائه می دهد. این مثال آموزشی نه تنها درک بازگشت را افزایش می دهد، بلکه بینشی را در مورد تفکر الگوریتمی برای حل پازل ارائه می دهد.

قوانین برج هانوی چیست؟
برج هانوی یک پازل ریاضی است که در آن سه میله و n دیسک داریم. هدف از پازل این است که کل پشته را به میله دیگری منتقل کنید، با رعایت قوانین ساده زیر: 

فقط یک دیسک را می توان در یک زمان جابجا کرد. 
هر حرکت شامل برداشتن دیسک بالایی از یکی از پشته ها و قرار دادن آن در بالای پشته دیگر است، یعنی یک دیسک تنها در صورتی می تواند جابجا شود که بالاترین دیسک روی یک پشته باشد. 
هیچ دیسکی را نمی توان روی دیسک کوچکتر قرار داد.
توجه: انتقال دیسک های n-1 بالایی از میله منبع به میله کمکی دوباره می تواند به عنوان یک مسئله جدید در نظر گرفته شود و به همان روش قابل حل است.

 

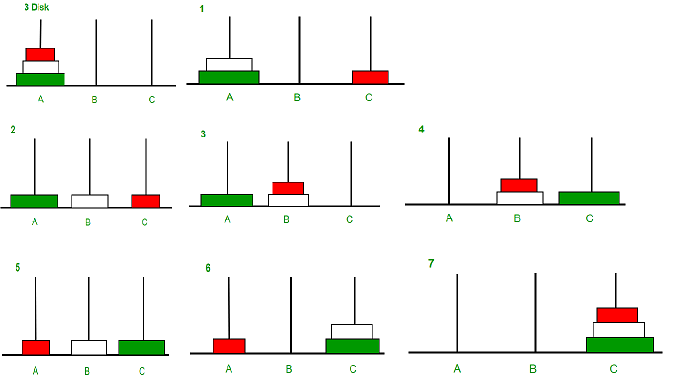
برج هانوی با استفاده از بازگشت
این تابع به صورت بازگشتی مشکل جابجایی n دیسک را به مشکلات کوچکتر متحرک n-1 دیسک تقسیم می کند. نقش میله ها (منبع، مقصد، کمکی) را در هر تماس بازگشتی جایگزین می کند تا انتقال گام به گام دیسک ها را طبق قوانین پازل برج هانوی تسهیل کند. قوانین این است که شما فقط می توانید یک دیسک را در یک زمان جابجا کنید و ممکن است دیسک بزرگتر روی دیسک کوچکتر قرار نگیرد.

# Recursive Python function to solve the tower of hanoi

def TowerOfHanoi(n , source, destination, auxiliary):
    if n==1:
        print ("Move disk 1 from source",source,"to destination",destination)
        return
    TowerOfHanoi(n-1, source, auxiliary, destination)
    print ("Move disk",n,"from source",source,"to destination",destination)
    TowerOfHanoi(n-1, auxiliary, destination, source)
        
# Driver code
n = 4
TowerOfHanoi(n,'A','B','C') 
# A, C, B are the name of rods

خروجی قطعه کد بالا بصورت زیر است:

Move disk 1 from source A to destination C
Move disk 2 from source A to destination B
Move disk 1 from source C to destination B
Move disk 3 from source A to destination C
Move disk 1 from source B to destination A
Move disk 2 from source B to destination C
Move disk 1 from source A to destination C
Move disk 4 from source A to destination B
Move disk 1 from source C to destination B
Move disk 2 from source C to destination A
Move disk 1 from source B to destination A
Move disk 3 from source C to destination B
Move disk 1 from source A to destination C
Move disk 2 from source A to destination B
Move disk 1 from source C to destination B

Time Complexity: O(2ⁿ)
Auxiliary Space: O(n)